理解關聯規則apriori算法:Apriori算法是第一個關聯規則挖掘算法,也是最經典的算法,它利用逐層搜索的迭代方法找出數據庫中項集的關系,以形成規則,其過程由連接【類矩陣運算】與剪枝【去掉那些沒必要的中間結果】組成。

理解關聯規則apriori算法:
一、概念
表1 某超市的交易數據庫
|
交易號TID |
顧客購買的商品 |
交易號TID |
顧客購買的商品 |
|
T1 |
bread, cream, milk, tea |
T6 |
bread, tea |
|
T2 |
bread, cream, milk |
T7 |
beer, milk, tea |
|
T3 |
cake, milk |
T8 |
bread, tea |
|
T4 |
milk, tea |
T9 |
bread, cream, milk, tea |
|
T5 |
bread, cake, milk |
T10 |
bread, milk, tea |
定義一:設I={i1,i2,…,im},是m個不同的項目的集合,每個ik稱為一個項目。項目的集合I稱為項集。其元素的個數稱為項集的長度,長度為k的項集稱為k-項集。引例中每個商品就是一個項目,項集為I={bread, beer, cake,cream, milk, tea},I的長度為6。
定義二:每筆交易T是項集I的一個子集。對應每一個交易有一個唯一標識交易號,記作TID。交易全體構成了交易數據庫D,|D|等于D中交易的個數。引例中包含10筆交易,因此|D|=10。
定義三:對于項集X,設定count(X?T)為交易集D中包含X的交易的數量,則項集X的支持度為:
support(X)=count(X?T)/|D|
引例中X={bread, milk}出現在T1,T2,T5,T9和T10中,所以支持度為0.5。
定義四:最小支持度是項集的最小支持閥值,記為SUPmin,代表了用戶關心的關聯規則的最低重要性。支持度不小于SUPmin 的項集稱為頻繁集,長度為k的頻繁集稱為k-頻繁集。如果設定SUPmin為0.3,引例中{bread, milk}的支持度是0.5,所以是2-頻繁集。
定義五:關聯規則是一個蘊含式:
R:X?Y
其中X?I,Y?I,并且X∩Y=?。表示項集X在某一交易中出現,則導致Y以某一概率也會出現。用戶關心的關聯規則,可以用兩個標準來衡量:支持度和可信度。
定義六:關聯規則R的支持度是交易集同時包含X和Y的交易數與|D|之比。即:
support(X?Y)=count(X?Y)/|D|
支持度反映了X、Y同時出現的概率。關聯規則的支持度等于頻繁集的支持度。
定義七:對于關聯規則R,可信度是指包含X和Y的交易數與包含X的交易數之比。即:
confidence(X?Y)=support(X?Y)/support(X)
可信度反映了如果交易中包含X,則交易包含Y的概率。一般來說,只有支持度和可信度較高的關聯規則才是用戶感興趣的。
定義八:設定關聯規則的最小支持度和最小可信度為SUPmin和CONFmin。規則R的支持度和可信度均不小于SUPmin和CONFmin ,則稱為強關聯規則。關聯規則挖掘的目的就是找出強關聯規則,從而指導商家的決策。
這八個定義包含了關聯規則相關的幾個重要基本概念,關聯規則挖掘主要有兩個問題:
- 找出交易數據庫中所有大于或等于用戶指定的最小支持度的頻繁項集。
- 利用頻繁項集生成所需要的關聯規則,根據用戶設定的最小可信度篩選出強關聯規則。
目前研究人員主要針對第一個問題進行研究,找出頻繁集是比較困難的,而有了頻繁集再生成強關聯規則就相對容易了。
二、理論基礎
首先來看一個頻繁集的性質。
定理:如果項目集X是頻繁集,那么它的非空子集都是頻繁集。
根據定理,已知一個k-頻繁集的項集X,X的所有k-1階子集都肯定是頻繁集,也就肯定可以找到兩個k-1頻繁集的項集,它們只有一項不同,且連接后等于X。這證明了通過連接k-1頻繁集產生的k-候選集覆蓋了k-頻繁集。同時,如果k-候選集中的項集Y,包含有某個k-1階子集不屬于k-1頻繁集,那么Y就不可能是頻繁集,應該從候選集中裁剪掉。Apriori算法就是利用了頻繁集的這個性質。
三、算法步驟:
首先是測試數據:
|
交易ID |
商品ID列表 |
|
T100 |
I1,I2,I5 |
|
T200 |
I2,I4 |
|
T300 |
I2,I3 |
|
T400 |
I1,I2,I4 |
|
T500 |
I1,I3 |
|
T600 |
I2,I3 |
|
T700 |
I1,I3 |
|
T800 |
I1,I2,I3,I5 |
|
T900 |
I1,I2,I3 |
算法的步驟圖:
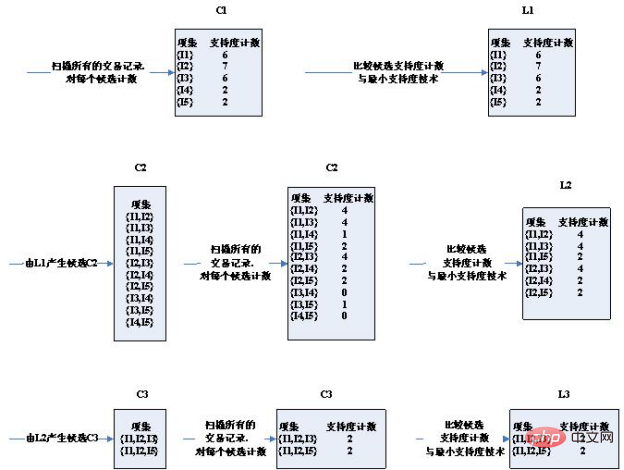
可以看到,第三輪的候選集發生了明顯的縮小,這是為什么呢?
請注意取候選集的兩個條件:
1.兩個K項集能夠連接的兩個條件是,它們有K-1項是相同的。所以,(I2,I4)和(I3,I5)這種是不能夠進行連接的。縮小了候選集。
2.如果一個項集是頻繁集,那么它不存在不是子集的頻繁集。比如(I1,I2)和(I1,I4)得到(I1,I2,I4),而(I1,I2,I4)存在子集(I1,I4)不是頻繁集。縮小了候選集。
第三輪得到的2個候選集,正好支持度等于最小支持度。所以,都算入頻繁集。
這時再看第四輪的候選集與頻繁集結果為空
可以看到,候選集和頻繁集居然為空了!因為通過第三輪得到的頻繁集自連接得到{I1,I2,I3,I5},它擁有子集{I2,I3,I5},而{I2,I3,I5}不是頻繁集,不滿足:頻繁集的子集也是頻繁集這一條件,所以被剪枝剪掉了。所以整個算法終止,取最后一次計算得到的頻繁集作為最終的頻繁集結果:
也就是:['I1,I2,I3', 'I1,I2,I5']
四、代碼:
編寫Python代碼實現Apriori算法。代碼需要注意如下兩點:
- 由于Apriori算法假定項集中的項是按字典序排序的,而集合本身是無序的,所以我們在必要時需要進行set和list的轉換;
- 由于要使用字典(support_data)記錄項集的支持度,需要用項集作為key,而可變集合無法作為字典的key,因此在合適時機應將項集轉為固定集合frozenset。
def local_data(file_path): import pandas as pd dt = pd.read_excel(file_path) data = dt['con'] locdata = [] for i in data: locdata.append(str(i).split(",")) # print(locdata) # change to [[1,2,3],[1,2,3]] length = [] for i in locdata: length.append(len(i)) # 計算長度并存儲 # print(length) ki = length[length.index(max(length))] # print(length[length.index(max(length))]) # length.index(max(length)讀取最大值的位置,然后再定位取出最大值 return locdata,kidef create_C1(data_set): """ Create frequent candidate 1-itemset C1 by scaning data set. Args: data_set: A list of transactions. Each transaction contains several items. Returns: C1: A set which contains all frequent candidate 1-itemsets """ C1 = set() for t in data_set: for item in t: item_set = frozenset([item]) C1.add(item_set) return C1def is_apriori(Ck_item, Lksub1): """ Judge whether a frequent candidate k-itemset satisfy Apriori property. Args: Ck_item: a frequent candidate k-itemset in Ck which contains all frequent candidate k-itemsets. Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. Returns: True: satisfying Apriori property. False: Not satisfying Apriori property. """ for item in Ck_item: sub_Ck = Ck_item - frozenset([item]) if sub_Ck not in Lksub1: return False return Truedef create_Ck(Lksub1, k): """ Create Ck, a set which contains all all frequent candidate k-itemsets by Lk-1's own connection operation. Args: Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. k: the item number of a frequent itemset. Return: Ck: a set which contains all all frequent candidate k-itemsets. """ Ck = set() len_Lksub1 = len(Lksub1) list_Lksub1 = list(Lksub1) for i in range(len_Lksub1): for j in range(1, len_Lksub1): l1 = list(list_Lksub1[i]) l2 = list(list_Lksub1[j]) l1.sort() l2.sort() if l1[0:k-2] == l2[0:k-2]: Ck_item = list_Lksub1[i] | list_Lksub1[j] # pruning if is_apriori(Ck_item, Lksub1): Ck.add(Ck_item) return Ckdef generate_Lk_by_Ck(data_set, Ck, min_support, support_data): """ Generate Lk by executing a delete policy from Ck. Args: data_set: A list of transactions. Each transaction contains several items. Ck: A set which contains all all frequent candidate k-itemsets. min_support: The minimum support. support_data: A dictionary. The key is frequent itemset and the value is support. Returns: Lk: A set which contains all all frequent k-itemsets. """ Lk = set() item_count = {} for t in data_set: for item in Ck: if item.issubset(t): if item not in item_count: item_count[item] = 1 else: item_count[item] += 1 t_num = float(len(data_set)) for item in item_count: if (item_count[item] / t_num) >= min_support: Lk.add(item) support_data[item] = item_count[item] / t_num return Lkdef generate_L(data_set, k, min_support): """ Generate all frequent itemsets. Args: data_set: A list of transactions. Each transaction contains several items. k: Maximum number of items for all frequent itemsets. min_support: The minimum support. Returns: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. """ support_data = {} C1 = create_C1(data_set) L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data) Lksub1 = L1.copy() L = [] L.append(Lksub1) for i in range(2, k+1): Ci = create_Ck(Lksub1, i) Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data) Lksub1 = Li.copy() L.append(Lksub1) return L, support_datadef generate_big_rules(L, support_data, min_conf): """ Generate big rules from frequent itemsets. Args: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. min_conf: Minimal confidence. Returns: big_rule_list: A list which contains all big rules. Each big rule is represented as a 3-tuple. """ big_rule_list = [] sub_set_list = [] for i in range(0, len(L)): for freq_set in L[i]: for sub_set in sub_set_list: if sub_set.issubset(freq_set): conf = support_data[freq_set] / support_data[freq_set - sub_set] big_rule = (freq_set - sub_set, sub_set, conf) if conf >= min_conf and big_rule not in big_rule_list: # print freq_set-sub_set, " => ", sub_set, "conf: ", conf big_rule_list.append(big_rule) sub_set_list.append(freq_set) return big_rule_listif __name__ == "__main__": """ Test """ file_path = "test_aa.xlsx" data_set,k = local_data(file_path) L, support_data = generate_L(data_set, k, min_support=0.2) big_rules_list = generate_big_rules(L, support_data, min_conf=0.4) print(L) for Lk in L: if len(list(Lk)) == 0: break print("="*50) print("frequent " + str(len(list(Lk)[0])) + "-itemsetsttsupport") print("="*50) for freq_set in Lk: print(freq_set, support_data[freq_set]) print() print("Big Rules") for item in big_rules_list: print(item[0], "=>", item[1], "conf: ", item[2])
文件格式:
test_aa.xlsx
name con T1 2,3,5T2 1,2,4T3 3,5T5 2,3,4T6 2,3,5T7 1,2,4T8 3,5T9 2,3,4T10 1,2,3,4,5
相關免費學習推薦:python視頻教程
 站長資訊網
站長資訊網