圖的應用:最短路徑
上篇文章的最小生成樹有沒有意猶未盡的感覺呀?不知道大家掌握得怎么樣,是不是搞清楚了普里姆和克魯斯卡爾這兩種算法的原理了呢?面試的時候如果你寫不出,至少得說出個大概來吧,當然,如果你是要考研的學生,那就要深入的理解并且記住整個算法的代碼了。
什么是最短路徑
今天我們學習的是圖的應用中另外一個經典的問題,也就是 最短路徑 的問題。這個問題和最小生成樹是不同的,最小生成樹的要求是要連通所有的結點,并且走得是權值最小的那條路線。而最短路徑則是指的從某個頂點到另一個頂點中權值最小的那條路徑。這條路徑不一定是包含在最小生成樹中的,所以它們并沒有太大的聯系。
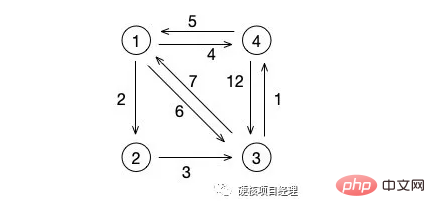
從這張圖來看,我們從結點 1 到結點 2 的最短路徑是 2 ,這個很明顯。那么從結點 1 到結點 3 呢?可不是直接的中間那個權值為 6 的路徑,而是走 1->2->3 這條路徑,也就是權值加起來為 5 的這條路徑。
然后我們再來看結點 3 ,它到結點 1 最短路徑應該是走 3->4->1 這條路徑,也就是權值為 6 的這條路徑,而不是中間的那條直線的權值為 7 的路徑。
沒錯,這就是最短路徑的概念了。在最短路徑中,我們一般會解決單向圖的問題,但實際生活中呢?最典型的地圖相關的應用其實是都是雙向圖的。不過這并不影響我們的學習,我們可以把這個示例圖中的結點看成是城市火車站點,就算是連接結點 1 和結點 3 的火車線路,也不一定來去的時間都是相同的。比如說從長沙到北京的 Z2 次火車全部運行時間為14小時42分,而回來的 Z1 次則是14小時10分。那么我們是否可以選擇其它的火車,比如有趟火車從長沙到石家莊可能只需要8小時,然后從石家莊到北京只需要2小時,這樣我們選擇這條線路的總時間就只需要10小時了(當然,這只是例子,大家在非高鐵的情況下肯定還是
 站長資訊網
站長資訊網